Thinking about learning objectives as a process of modeling
1 - Modeling begins before you ever touch a computer
- How do I understand the system of interest?
- Within that system, what phenomena am I interested in?
- What entities do I think are relevant for my model?
- How might I qualitatively describe entity relationships in the model? (Example: predators hunt prey, so predators should have some contribution to the reduction of prey.)
- What simplifications do I know I’m making?
- How can I express expectations of/predictions about the model? (E.g., with one wolf and 10 million rabbits, I don’t think there will be much of a predator effect. Or: here’s a sketch of the path I think this orbiting body might take. Or: based on my experiences with kerbal space program, I figure the object would take a path like this.)
1.1 For a given situation-to-be-modeled, Students will be able to
- describe one or more phenomena they want their model to address.
- state and justify (with words, pictures, gestures) which entities they care about for this model. . (“Our model needs to include/account for __ because __). This can also be phrased as state and justify the inclusion of entities in their model
- identify and justify simplifications their model makes. (Our model ignores air resistance because ___)
- qualitatively describe entity relationships in the model. (E.g., the traffic jam may propagate backwards through traffic, because each car won’t decelerate until it’s within x of the rear bumper of the car in front. Or: roughly speaking, a wolf will seek a rabbit if it finds one, and a rabbit will evade a wolf if it detects one.)
- predict or hypothesize how the model may behave (E.g., If we give cars on the highway high initial speeds and a very low braking distance threshold (how far from the next car they’ll be before they start decelerating), there will be guaranteed crashes. Or: If rabbits are fast and can hear wolves coming from far away, the wolves won’t be successful predators. But, if we can somehow get the wolves to hunt as a pack and surround a rabbit, they should be better able to catch rabbits.) One way we might start to assess this is “if you wanted to tweak the simulation to make the wolves better hunters without changing the rabbit behavior, what might you do?” Or “suppose the wolf population could adapt and become more efficient at hunting rabbits. Give an example of a new behavior you might give them to hunt more efficiently and show in pseudocode how you might roughly encode the behavior into the model.)
2 - Formalizing the model
- What are different ways we might encode/represent a model? (difference equations? Python Code? stock/flow/converter diagrams? other diagrams?)
- For many of the models we’ll build, we’ll need to be able to express behaviors, do some calculations, and store/move/manipulate some data. In service of those aims, in Python, how can we
- Store information for use later?
- Represent numbers and convert between their forms? (Int, Float)
- Perform operations on numbers (for example, arithmetic. If you’ve never programmed before,
*as the multiplication operator may not be obvious) - Represent letters/words?
- Perform operations on letters/words? (Find regular patterns, make substitutions, convert case, concatenate, split)?
- Create data by composing words/letters and numbers? (Lists are ordered like trains. Dicts are kind of like buckets of labeled stuff.)
- Perform repeated operations on those compositions, including iteration. (If we learn primitives and manipulating primitives, then it makes sense to learn compositions and manipulating compositions.)
- Bundle up repeated operations so they’re easier to invoke/apply later (function definition)
- Pull in external collections of bundled-up procedures (import other modules/packages/libraries)
- For many of the models we’ll build, we’ll try to take advantage of specific advantages we get for free with SciPy and NumPy. In SciPy/NumPy how can we:
- Get statistical information about a collection of numerical data. (the
max,min,cumsum,varandmeanmethods ofndarray, for example) - Perform operations using the numbers in a collection (the
summethod of anndarray, for example) - Iterate over an array of data (
numpy.nditer?) - // Fill in more objectives here
- Get statistical information about a collection of numerical data. (the
- How can we see different representational forms as comparable articulations of the same model?
- How do changes to one representation of a model correspond to changes in one or more other representations?
- If we change a relationship in a model diagram, how does that affect any difference equations we might have written?
- How do changes to one representation of a model correspond to changes in one or more other representations?
- What are the different kinds of engines/paradigms that can drive models?
- Deterministic systems with a centralized parameter (such as time), where objects in the model update in response to discrete, progressive changes to that parameter. Here, our main task is to specify update procedures as functions of the parameters of the system.
- Stochastic (dice rolling) processes, where we inject elements of randomness and/or probability
- Why would we want to make a model non-deterministic?
- Why would we include randomness?
- Agent-based Modeling, where we’re trying to produce simple rule-based behavior to govern individual parts of the system. Rather than thinking of these as system-wide updates based on parameters, we can think of this as individual agents reacting to their own state and what’s around them.
- Markov Chain Monte-Carlo
2.1 When it comes to formalizing models, students will be able to
In Scratch:
- Use triggers (events) to start/stop a program
- Write a top-level comment on code
- Write a code comment attached to a specific block
- Identify different datatypes (booleans, expressions, strings)
- Use abstractions for iteration (repeat functions) to perform a task multiple times
- Use control flow to create conditional branching in code
- Create a variable and access its contents
- Create a list
- Add an item to a list
- Delete an item from a list
- Replace an item in a list
- Use positional indexing to retrieve a list item
- Retrieve a slice/subsection of a list
- Print debugging output using the “say” block (which, confusingly, is under “Looks”)
- Use operations to add, subtract, and multiply two numbers
- Write an (in)equality test in terms of one or more variables
- Refactor repetitive code using abstraction
- Define blocks (functions) that wrap chunks of procedures
- Predict, Observe, and Explain/Reconcile what a short scratch program (~10 blocks or fewer) will do
In base Python:
- Store information for use later
- Retrive Stored Information
- Represent numbers and convert between their forms (
Int,Float) - Perform operations on numbers (for example, arithmetic. If you’ve never programmed before,
*as the multiplication operator may not be obvious) - Represent letters/words
- Perform operations on letters/words (Find regular patterns, make substitutions, convert case, concatenate, split)?
- Create data by composing words/letters and numbers (Lists are ordered like trains. Dicts are kind of like buckets of labeled stuff.)
- Perform repeated operations on those compositions, including iteration. (If we learn primitives and manipulating primitives, then it makes sense to learn compositions and manipulating compositions.)
- Bundle up repeated operations so they’re easier to invoke/apply later (function definition)
- Pull in external collections of bundled-up procedures (import other modules/packages/libraries)
In NumPy / Pandas
- Get statistical information about a collection of numerical data. (the
max,min,cumsum,varandmeanmethods ofndarray, for example) - Perform operations using the numbers in a collection (the
summethod of anndarray, for example) - Iterate over an array of data (
numpy.nditer?) - // Fill in more objectives here
- Across Formal Models:
- Express and discuss relationships between difference equations and a model produced in code(?)
Across different formalisms of a model:
- Describe how a given piece of code implements a relationship
- Determine whether a piece of code faithfully implements part of a model expressed in some other format (diagram, difference equation)
- Across Formal Modeling Paradigms:
- Describe and compare the mechanisms of
- Deterministic systems with a centralized parameter (such as time), where objects in the model update in response to discrete, progressive changes to that parameter. Here, our main task is to specify update procedures as functions of the parameters of the system.
- Agent-based Modeling, where we’re trying to produce simple rule-based behavior to govern individual parts of the system. Rather than thinking of these as system-wide updates based on parameters, we can think of this as individual agents reacting to their own state and what’s around them.
- Markov Chain Monte-Carlo
3 - Interrogating the model
How we think about interrogating the model
- How do I figure out what’s happening when I run my model?
- What information can I get about my model?
- What diagnostic plots can I get from my model?
- lines/functions of best fit
- residuals
- histograms
- What numerical summaries can I get from my data?
- 5-number summary (Tukey)
- Measures of central tendency/typicality
- Measures of variation
- Extrema and outliers
- (if available) tables of predicted-vs-actual model results for Supervised learning situations
- What diagnostic plots can I get from my model?
- How does my model behave in extrema/limiting cases?
- What are some ways I could generate random data to throw at this model?
- How can I generate extreme data? What would that mean?
- Is this model answering the question I want to ask?
- In retrospect, does what comes out of the model echo how the real system behaves/should behave?
- What statements can I make (in plain writing, say English) about the performance of my model?
3.1 Learning Objectives: For a given model, students will be able to
- Enumerate some techniques (visual, numerical, or other) for interrogating a model. Examples would include calculating a measure of central tendency, plotting actual data vs. model fit, creating distribution diagrams/histograms/kernel density estimates.
- implement at least two different interrogation techniques:
- describe the model’s faithfulness (if it’s time-based, what’s the long-run behavior? if it’s statistical, where do the data depart from the model? If it’s non-parametric, what insight do we get from it?)
- Identify the error in their models, through (for example) tabular summaries of residuals, cumulative residual plots, smoothing and confidence intervals. Example:
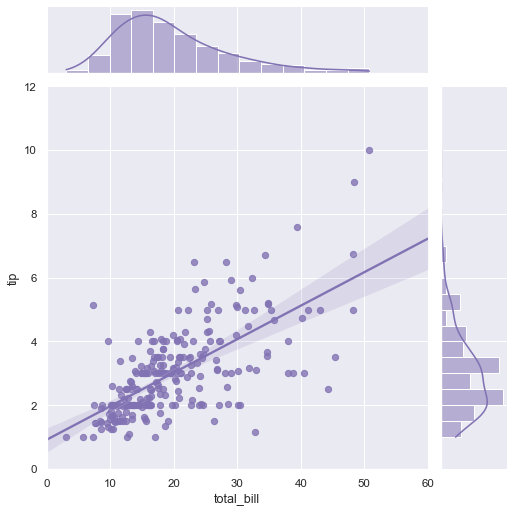 .
. - Create a plot to assess model fit
- Judge and justify the appropriateness of a model using diagnostic plots (and justify their reasoning)
4 - Refining the model
- How do I achieve a better fit?
- What constitutes a “better fit?”
- How do I think about the complexity of my model?
- What is model complexity?
- Should I add terms to my model?
- Should I change the value of any of the input parameters?
- Should I add interactions to my model?
- Should I rethink the mathematical relationships I’ve posed? (the data looks nonlinear, but I’m attempting a linear fit)
- How do I understand the trade-off between interpretability and model complexity?
- If I make the model more complex, how will that impact:
- The time it takes to program/debug
- The time it takes to actually execute on a computer
- The time it takes to interpret/make sense of the results?
- What’s the least I can do to make my model useful? What’s the minimal amount of complexity I need to encode to get something useful?
- What information are my diagnostics giving me?
- How do I think about model refinements in light of that information
4.1 - Learning Objectives: Students will be able to
- compare two variations of a model (say, a linear model and a quadratic model) and argue for which model better captures the phenomenon
- For a given model, interpret their model qualitatively
- For a given model, suggest and justify a refinement to it
5 - Sharing/publicizing the model (reproducible research/open science)
5.1 - Learning Objectives: Students will be able to
- Create an iPython Notebook that mixes both Python code and explanatory markdown
- Share an iPython Notebook using NBconvert / NBviewer
- Download someone’s existing iPython Notebook
- Possibly by forking the repository
- review someone else’s code
- modify their own fork of the upstream repository
- justify their modifications
- Issue a pull request on the upstream repository
6 - Assessing/Comparing/Debating models
// Some of the really cool intellectual meat. Given the kind of diagnostic information we get (cluster 3) and possibly being able to share our models (cluster 5), how do we make decisions about how well the model is working and whether to refine it (cluster 3). This is where we get into the work of justifying a model we’ve built, exploring whether our asusmptions (cluster 1) held sway, and so on.
// 2015-08-26 - I actually think much of this is covered by the first 5 clusters :-/
7 - Data Science
Understanding data
- Determine the feature-space (what are the columns?)
- Make a dataset tidy
- Get numerical summaries of data (mean, median, mode, variance)
- Create a procedure for a statistic (mean, median, mode)
- Visually and numerically examine correlations between features
- Filter a dataset’s rows by some condition, for example
flint_data[flint_data['lead_levels'] > legal_limit] - Group a dataset by categorical values (
flint_data.groupby('zip_code').sum()) - Generate a by-group analysis based on values of a feature (for example, with aggregate statistics like sum, count, mean)
- Given a dataset, fit a parametric model to the data
- As in modeling, assess the fit, faithfulness, and limitations of the model
Plotting
- Plot and interpret a distribution of 1-variable
- Plot and interpret a graphic of multiple variables [scatterplot, box-and-whiskers, pie chart, time series, line graph, bar graph, compositions of plots, experimental scatterplot, subplots, contour plot]
- Use aesthetics to encode multiple dimensions of information into a single plot (e.g., using stroke-color, shape, size, fill-color, opacity, and line-type to encode additional information)
- Use small multiples to encode multiple dimensions of information into a single plot (facetting by a variable, for example, or a scatterplot matrix
Fitting a model to data
- Describe the iterative process of updating the state of a variable
- Recognize the relationship between a differential equation, difference equation, and state-update code in a model
- Given a 2-dimensional dataset, try choosing parameters to minimize ordinary least squares error
- Enact a gradient descent by playing the role of a walker (blindfolded student) and a guide (who gives gradient information). See “Gradient Descent Activity”
- Write a simple python program to do gradient descent on a slope-intercept linear model
- Use scikit-learn’s stochastic gradient descent to fit a multi-feature linear model (multiple linear regression)